几乎所有文件系统索引,数据库索引,都需要用到B-tree或其变种。因此对于码农而言,理解它如何工作还是相当有必要的。然而我最近阅读了很多相关的文章,它们往往一上来就试图跟读者解释
branchingFactor/degree, B-1<=keys<2B-1,B<=children<2B blablabla...,在读者还不懂原理时就开始描述实现细节。导致像我一样没学过正统cs课程的野生码农严重怀疑自己的智商。这篇文章试图向跟我一样的小白来描述B-tree(前提是你能理解二分查找)。
一.B tree,B-tree,B+tree
如果你在google搜索B-tree数据结构,你可能会找到以上三个关键字相关的文章,这一度让我觉得它们是三种不同的数据结构(既然有BPlusTree,很容易让人想到还有BMinusTree,再加上一些不负责任的翻译版算法书竟然丧心病狂的使用 B- tree (注意空格)来标识B-tree)。事实上这里的 - 只是连字符,B-tree与B tree是同一回事。而B+tree则是它们的一个演化版。当然你也许还会发现一些文章中的B-tree和另一些文章中的B tree有着不同的实现。请依然不要被误导,我读了大概20来篇B-tree相关的文章,至今没有发现两个完全相同的实现。。。
二.Trees
BinarySearchTree
下图展示的是一颗完全平衡的二叉树,每个节点大于其左子节点,小于其右子节点。当需要查找每个键时,先将其与根节点比较,如果小于根节点则继续查找根节点的左子树,否则查找右子树。如果你对该过程还不熟悉,建议先花一些时间看一些入门的算法教程。在理想情况下(如图所示完美平衡的情况下),一颗含有N个节点的二叉树,其高度正好为 $\log (N+1)$。这意味着一次查找最多只会经过 $\log (N+1)$ 个节点。举例来说如果一颗平衡二叉树包含1000个元素,那么树的高度为10,一次查找操作最多经过10个节点。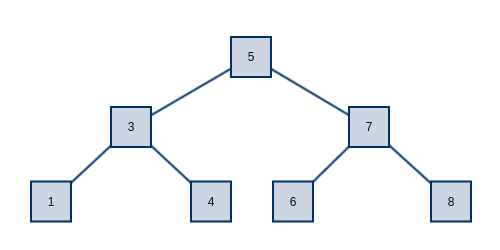
2-3tree
接下来,人们发现在每个节点中添加一个key,该算法同样高效。如下图所示,一个节点可以有两个key和三条链接,人们亲切的称其为2-3树。2-3树的查找算法与二叉树如出一辙,但由于每个节点可以多存储1个key,进一步降低了树的高度(降低树高并不是2-3树的主要目的,主要目的在于自平衡)。很容易可以得出结论,一棵含有N个节点的2-3树其高度在 $\log N$ (2-3数允许包含只有一个key的节点)和 $\log _3N$ 之间。也就是说一棵含有10亿个key的2-3树,其高度在19到30之间。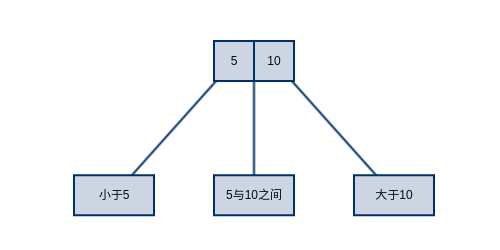
RedBlackTree(乱入)
2-3树对比二叉树的主要优势在于,为了在插入数据时维护树的平衡,你不必再深陷于节点间的左旋转,右旋转无法自拔。2-3树只有根节点分裂的情况下会增加树的高度(这篇文章只谈搜索,对插入与删除感兴趣可以查看文章末尾的链接)。而它的一个缺点在于,在实现中要抽象这种既可能有一个key,又可能有两个key的节点有些繁琐,于是出现了下图所示的数据结构。所有的节点再度回归到只有一个key,并通过两个节点来组成一个含有两个key的节点。为了区分它们与普通二叉树节点的不同,将它们之间的链接标记为红色。江湖人称红黑树。下图所示的红黑树完全等价于上面的2-3树。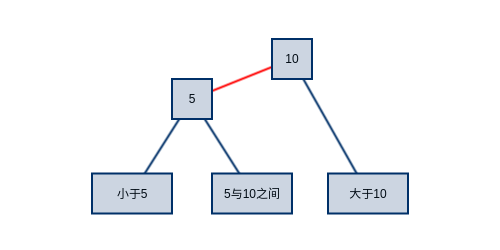
B-tree
既然我们可以在每个节点中添加一个key,那为什么不干脆添加多个key?于是就出现了类似下图的数据结构,也就是本文的主角B-tree。在B-tree中一个节点可以保存多个key,但具体可以保存多少个key必须有一个参数来加以控制,如果一个节点可以保存无限个key,那它就跟链表没什么区别了,太少又达不到降低树高的效果。接下来,我们需要为这个参数取一个高大上的名字,好让它可以糊弄那些初学者,比如说branchingFactor或者degree就都还不错,在本文中将使用branchingFactor(简写为B)标识该参数,并约定每个节点的key数量大于等于B-1,小于2B-1。这样一来,我们就可以说一棵2-3树是一棵B等于2的B-tree了。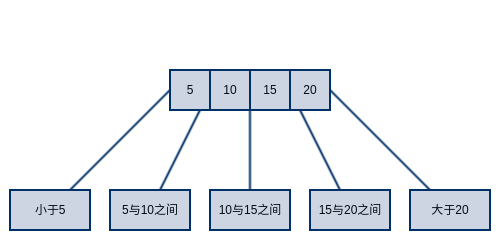
小结
上面的树结构各式各样,但查找元素的算法都大同小异,无非是利用每次比较的信息量来确定下一步要查找的分支。用我这个野生程序员的话来总结就是:2-3tree是B等于2的B-tree,红黑树是2-3树的一个特殊实现,同时还是一颗平衡二叉树。至于 rotate,flip,split 什么的,让它随风去吧。
三.why B-tree?
由于每个节点可以保存多个key,B-tree的高度通常非常低,当B等于500时,一颗含有625亿个key的B-tree高度不会超过4。然而这并不意味B-tree拥有比平衡二叉树更优的查询复杂度。假设一颗含有N个元素的B-tree每个节点正好保存了B个key,那么一次查询最多经过 $\log _BN$ 个节点,但在每个节点中需进行一次二分查找确定下一步选择哪个节点,因此B-tree查找算法实际的时间复杂度为 $O(\log _BN \times \log B)$,熟悉对数性质的同学能够看出来该值就等于 $O(\log N)$。既然如此,为什么还需要B-tree?。
上面的计算模型假设对存储器的每一次读取操作成本是相等的。但实际情况往往并非如此。最简单的例子就是,一次磁盘读取操作的开销要比内存读取大好几个数量级。为了尽量减少磁盘IO的次数,往往每次读取磁盘会额外预读一部分数据到内存中,预读数据以页(又称为簇,NTFS文件系统中默认簇大小为4096字节)为单位。也就是说当你需要在磁盘中读取1个字节的数据,计算机会在磁盘中找到该数据,并以其为起始位置一次性读取多页数据载入内存备用。这样一来如果一个树节点所占空间正好为一页大小,就能保证访问该节点所有key值只会发生一次磁盘读取。按照该理论,如果一页能够容纳1000个key节点(B=500),那么在容纳数百亿key值的B-tree中,最多3次磁盘读取就能完成一次查询操作(根节点一般常驻内存),而一般的二叉树显然无法保证这一点。
四.why B+tree?
为了更好的利用B-tree的优势,必须确保一个树节点所占空间小于文件系统页。也就是说假设一个B-tree节点中的key数量为n,必须保证 pageSize >= n(keySize + dataSize + pointSize) + pointSize 。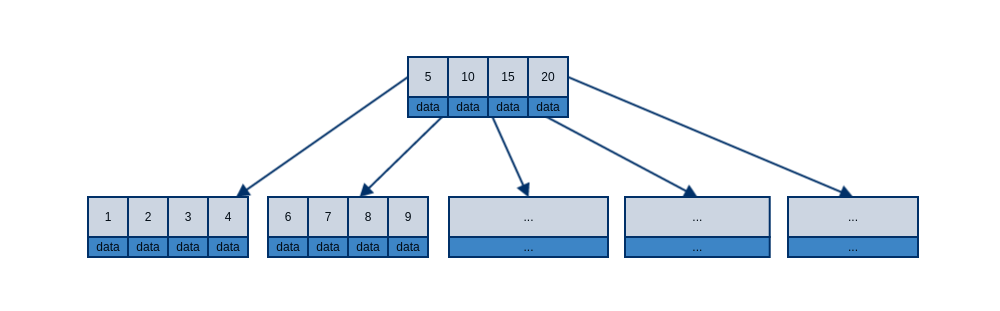
上图展示了一个典型的B-tree节点,其中最大的问题在于,如果data所占空间太大,那么我们不得不选择一个较小的B值,而B值过小又无法保证合理的树高。更加麻烦的是,在实现B-tree时,我们往往并不知道data有多大。考虑到上述这些困境,B+tree应运而生。下图展示了典型的B+tree节点,其中最大的变化在于,内部节点不再保存数据,因此每个内部节点得到了更多的空间来存储key值,进一步发挥了B-tree的优势。同时外部节点的实现也有了更多的想象空间,它可以是硬盘中的一页数据,也可以是网络中的某台计算机。如果是用来实现数据库索引,通常还会在外部节点之间添加指向下一节点的指针,这样可以更好的支持范围查询操作。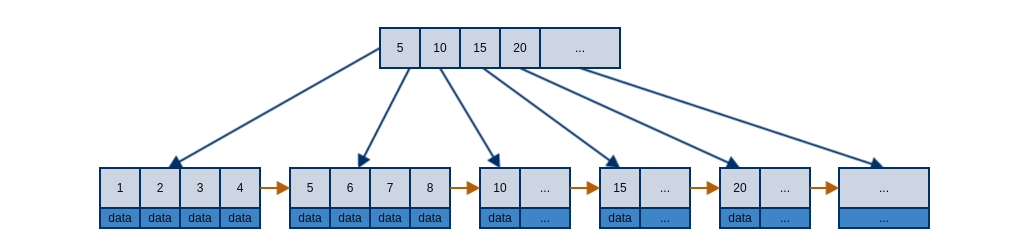
五.总结
以上内容仅仅介绍了B-tree的基本结构以及它要解决的问题,不过我认为对于入门玩家来说,这就足够了。想要更加深入理解或是自己实现B-tree的读者可以查看下面的链接。最后附上我的 B+tree(typescript) 实现以供参考。
