一直不明白计算机如何通过软件实现乘法,除法,开方等常见的数值运算,最近我在mit开源课程中得到了答案,以下是学习心得。
一.乘法运算
1.暴力算法
假设有两个十进制数x=12345678,y=87654321,我们需要计算x与y的乘积,可以先采用分治(Divide and Conquer)的思想,将每个数字拆分成两半,如下表所示:
| 1234 | 5678 |
|---|---|
| $x_0$ | $x_1$ |
| 8765 | 4321 |
|---|---|
| $y_0$ | $y_1$ |
很容易得到:$$x=10^{d/2}x_0+x_1=12340000+5678$$$$y=10^{d/2}y_0+y_1=87650000+4321$$$$\Rightarrow xy=(10^{d/2}x_0+x_1)(10^{d/2}y_0+y_1)$$$$\Rightarrow xy=10^dx_0y_0+10^{d/2}(x_0y_1+x_1y_0)+x_1y_1$$这样下来每一次递归,都可以把两个数的乘积,转换成四组更小精度数的乘积之和,重复这个过程直到把问题划分成多个个位数的乘积之和,这个时候简单的使用九九乘法表就能得到每一项的结果。整个过程其实与我们小学学的计算方式很类似,你可以在草稿纸上尝试计算12*34来模拟这个过程。
当然,以上是人类的思维方式,把上面的数字转换成相应的二进制数就能模拟计算机的思维方式,唯一的不同是计算机的个位数相乘不需要乘法口诀,进行一次位与(&)运算就可以了。下面是它的时间复杂度(计算过程与一般分治算法复杂度计算过程类似,下文不再提及):$$T(N)=4T(N/2)+\Theta(N)=\Theta(N^2)$$
2.Karatsuba算法
上面的暴力算法将x乘以y拆分成了$x_0y_0,x_0y_1,x_1y_0,x_1y_1$四个更小规模的子问题,而一名叫Karatsuba的学者发现,在已知$x_0y_0,x_1y_1$的情况下,可以使用$(x_0+x_1)(y_0+y_1)-x_0y_0-x_1y_1$来得到$x_0y_1+x_1y_0$的值,整个算式变成了:$$xy=10^dx_0y_0+10^{d/2}[(x_0+x_1)(y_0+y_1)-x_0y_0-x_1y_1]+x_1y_1$$这样每次递归调用只需要进行三次乘法运算,此时复杂度为:$$T(N)=3(T/2)+\Theta(N)=\Theta(N^{\log_23})\approx\Theta(N^{1.58})$$在Karatsuba之后,Toom-Cook通过每次将数字切分成多个部分进一步提升了算法的性能,例如将前面的x切分成$x_0,x_1,x_2$三个部分,此时算法的复杂度为:$$T(N)=5(T/3)+\Theta(N)=\Theta(N^{\log_35})\approx\Theta(N^{1.46})$$Schönhage–Strassen通过快速傅里叶转换将复杂度提升至$\Theta(NlogNloglogN)$,但这些显然只有在精度需求非常大的情况下才有意义。大部分情况下使用暴力算法或Karatsuba算法就已经足够了。
二.牛顿法(Newton-Raphson method)
牛顿法是一种求解方程近似根的方法,他在计算机领域应用非常广泛,下文要提到的除法运算与开方运算都需要通过它实现。下面是方法的简介:
假设现在我们需要计算函数f(x)的根(当f(x)取0时,x的值称作方程的根)
1.先取一个大概的值$x_0$,代入该函数可以得到$y_0$
2.过$(x_0,y_0)$作一条切线,该切线的斜率为$f'(x_0)$(这里$f'$表示函数$f$的导数)
3.计算该切线与x轴的焦点$x_1$,显然这里有:$$k=\frac{y_0}{x_0-x_1}=f'(x_0)=\frac{f(x_0)}{x_0-x_1}$$$$\Rightarrow x_1=x_0-\frac{f(x_0)}{f'(x_0)}$$
4.重复上面的过程,直到得到令你满意的精度为止。wikipedia上的这张图清晰的展示了它的迭代过程:
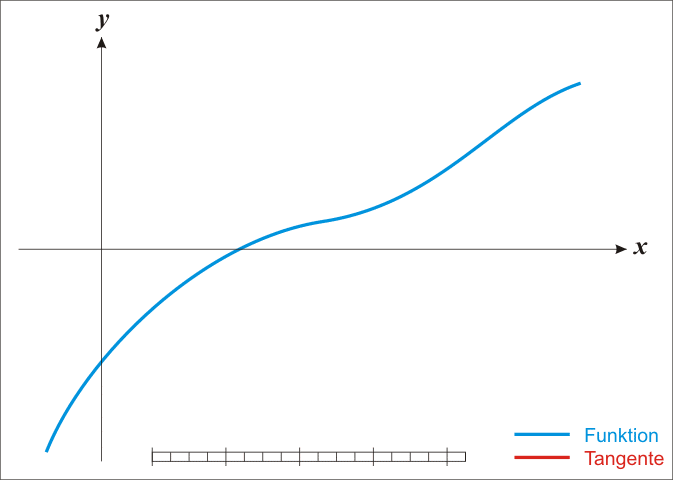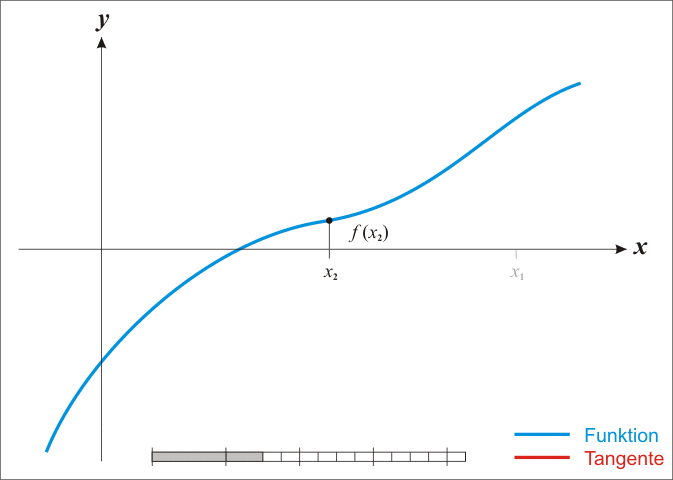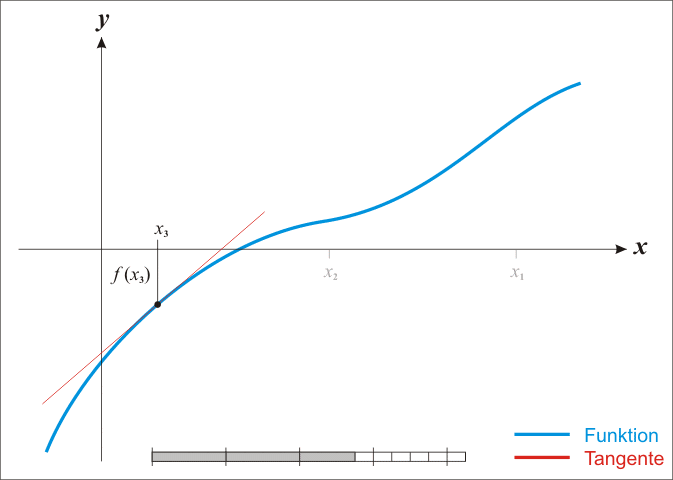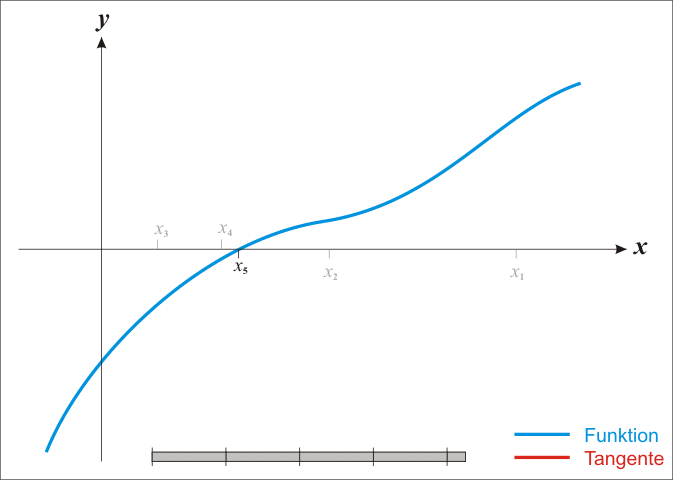
三.平方根算法
牛顿法的一个常见的应用场景是计算算术平方根,现在假设我们需要计算$\sqrt{a}$的值,这等价于计算$f(x)=x^2-a$的根,将其代入上面的公式可得:$$x_1=x_0-\frac{f(x_0)}{f'(x_0)}=x_0-\frac{x^2-a}{2x}=\frac{x_0+a/x_0}{2}$$用java代码来简单模拟求解过程:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21public static double sqrt(double input){
double x=input;
for (int i = 0; i < 5; i++) {
x=(x+input/x)>>1;
System.out.println(i+"次迭代:"+x);
}
return x;
}
public static void main(String... args){
sqrt(2d);
/*
参考值 :1.414213562373095
程序输出:
0次迭代:1.5
1次迭代:1.4166666666666665
2次迭代:1.4142156862745097
3次迭代:1.4142135623746899
4次迭代:1.414213562373095
*/
}
大部分情况下,牛顿法具有平方级的收敛性能,即每迭代一次,结果的有效数字将增加一倍,这意味着只需要logN次迭代就能得到N精度的结果。但我们不能说它的复杂度是对数级的,因为我们忽视$a/x_0$这项操作,要知道以上算法的复杂度,必须先来看看除法运算的复杂度。
四.除法运算
假设我们需要计算a/b,我们可以先将a/b转换成$a\frac{1}{b}$,由于乘法操作是已知的,因此这里只需要计算1/b就可以了,接下来可以构建一个函数$f(x)=\frac{1}{x}-b$,然后继续用牛顿法求它的根:$$x_1=x_0-\frac{f(x_0)}{f(x_1)}=x_0-\frac{1/x_0-b}{-1/x_0^2}=x_0(2-bx_0)$$这样就把除法运算全部转换成了乘法运算,同样我们需要logN次迭代才能得出N精度的结果,这里假设乘法运算的复杂度是$N^\alpha$,于是可以简单的得出复杂度的上界是$N^\alpha logN$,但仔细观察会发现,并不是每一次迭代都需要进行N精度的乘法,更准确的复杂度推导如下:$$T(N)=1^\alpha+2^\alpha+4^\alpha+8^\alpha+\cdots+N^\alpha$$$$\Rightarrow T(N)=(2^\alpha)^0+(2^\alpha)^1+(2^\alpha)^2+\cdots+(2^\alpha)^{logN}$$$$\Rightarrow 2^\alpha T(N)=(2^\alpha)^1+(2^\alpha)^2+\cdots+(2^\alpha)^{logN}+(2^\alpha)^{logN+1}$$$$\Rightarrow (2^\alpha-1)T(N)=(2^\alpha)^{logN+1}-(2^\alpha)^0$$$$\Rightarrow T(N)=\frac{(2N)^\alpha-1}{2^\alpha-1}=\Theta(N^\alpha)$$最终得出结论,使用牛顿法进行除法运算其复杂度与所用的乘法算法复杂度一致,类似的,容易证明使用牛顿法计算平方根的时间复杂度也是$\Theta(N^\alpha)$。
以上是这篇文章的全部内容,下篇文章来介绍一个神奇的平方根倒数算法,其中同样涉及到牛顿法。
